A study is underway to determine the nature of errors that result when fields with sharp vertical gradients are interpolated from model levels to the standard AMIPII pressure levels. Results will be examined with the LLNL/UCLA, LMD, and NCAR/CCM3 models. There are really two questions regarding vertical interpolation that must be addressed:

1) What is the effect of the order of interpolation (i.e., averaging on model coordinates and then interpolating to standard pressure levels or interpolating to standard pressure levels every sampled time step and then averaging) ?

2) Should fields that may contain sharp vertical gradients (e.g., cloud related fields) be interpolated to the standard pressure levels?

Here with focus on the second question.

The CCM3 monthly mean data were available on the model sigma/pressure hybrid vertical coordinate. Using the surface pressure at each gridpoint, the corresponding pressure level at each gridpoint was determined. These data were then linearly interpolated to the 17 AMIP pressure levels. Although more sophisticated interpolation techniques might be used, it was felt at this stage to keep this aspect of the study very simple. Additionally, the model pressure data (ie, the equivalent pressure of the monthly mean eta coordinate levels) and the AMIP interpolated data were linearly interpolated to a very fine vertical grid of 5 mb spacing. This was done to allow differences to be computed.

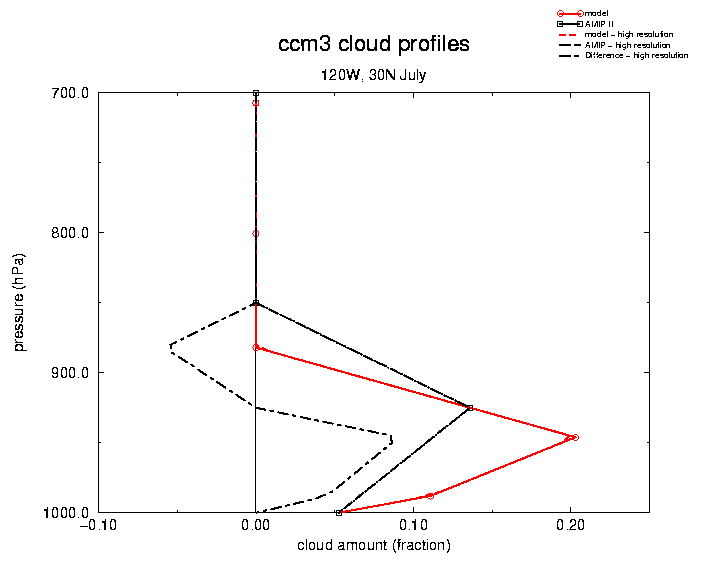
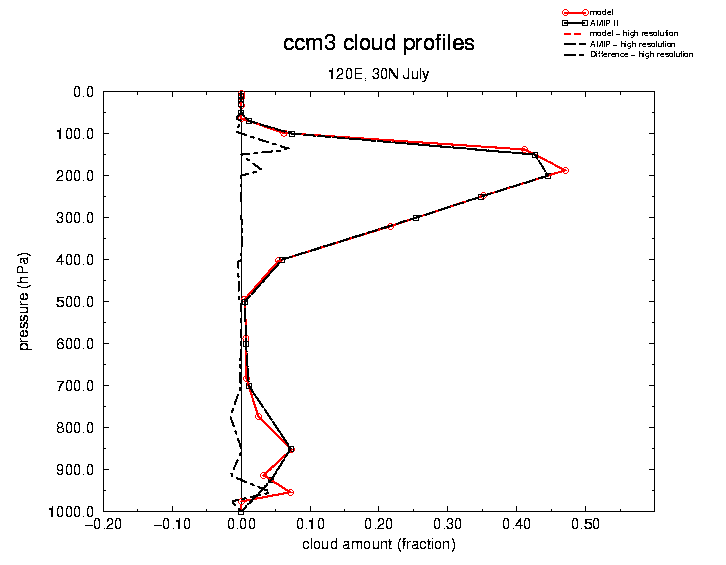
Figure 1 is a profile taken over the position of the West Pacific warm pool, (150E, 0N). There are five curves plotted. The model data (red line) the model data interpolated to the AMIP levels (black line), the model data interpolated to the high resolution vertical grid (dashed red), the AMIP level data interpolated to the high resolution grid (black dashed) and the difference between the last two (dash-dot black). The plot indicates the obvious problem with discrete data such as clouds, where the model levels and AMIP levels nearly coincide there is good agreement, but a relatively small misalignment in the levels can generate very significant discrepancies. The CCM3 and the AMIP levels have the largest mismatch in the lowest levels. Below 800 mb the model has nominally 5 levels while the AMIP standard levels have 3. This can lead to problems as shown in Fig. 2, which is the cloud profile at 120W, 30N. This region was chosen because in had persistent low cloud in July. The mismatch between the model and the AMIP levels can lead to fairly serious errors at lower levels. Figure 3 is a cross section of the CCM3 cloud amount for July along 180E from 70N to 20S, also plotted are the contours of the errors generated by interpolating to the AMIP levels. The errors are not correlated well with cloud fraction but are critically dependent on cloud position with respect to the AMIP levels. In the North Pacific, where there is persistent low cloud there are large errors, yet the errors are less in the equatorial regions where the AMIP levels have sufficient resolution to capture the model cloud distribution.

As might be anticipated the nature and size of the errors are sensitive to the model vertical structure and its relation to the AMIP levels. The figures indicate that the AMIP interpolated data can lead to significant misrepresentation of the cloud distribution. Similar error distributions are seen in variables sensitive to cloud location, such as long wave radiational heating.